Aduana: Link Analysis With Frontera | Zyte

Valdir Stumm Junior

10 Mins

June 8, 2015

Aduana: Link analysis with Frontera

It's not uncommon to need to crawl a large number of unfamiliar websites when gathering content. Page ranking algorithms are incredibly useful in these scenarios as it can be tricky to determine which pages are relevant to the content you're looking for.

In this post we'll show you how you can make use of Aduana and Frontera to implement popular page ranking algorithms in your Scrapy projects.

Page ranking algorithms and Frontera

Aduana is a library to track the state of crawled pages and decide which page should be crawled next. It is written in C but is wrapped in Python to use it as a Frontera backend. We intend it to be the backend for a distributed crawled, where several spiders ask for the next pages to be crawled.

The driving force behind Aduana design has been speed: we want it to operate fast even when serving multiple spiders even when billions of links have already been discovered. Speed must be maintained even when executing relatively complex algorithms like PageRank or HITS scoring.

Right now, Aduana implements a Best First scheduler, meaning that pages are ordered by a calculated score and the page with highest score is selected to be crawled next. Once a page has been crawled it's never crawled again. Scores in Aduana can be computed in several different ways:

Using PageRank.
Using HITS (authority score is used).
Using specific scores, provided by the spider for each page. For example by analyzing page content although arbitrary scores can be used: URL length, crawl depth, domain alphabetical ordering, whatever.
Using a mix of specific scores and PageRank or HITS.

The advantage of using PageRank or HITS is that they are not application specific, however they can wander off-topic when crawling for a large time and they are computationally more expensive.

Using specific scores give good results but requires fine tuning the algorithm, for example, to make it robust against content spam pages. On the plus side, they are computationally cheap, at least with Aduana.

Finally, merging specific scores with PageRank or HITS might give the best of both worlds in terms of accuracy, at the same computational cost that running plain PageRank or HITS.

To understand how PageRank and HITS are merged with specific scores we first need to understand the plain algorithms.

PageRank

PageRank is perhaps the most well known page ranking algorithm. The PageRank algorithm makes use of the link structure of the web to calculate a score which can be used to influence search results. PageRank is one of Google’s methods for determining a page’s relevance.

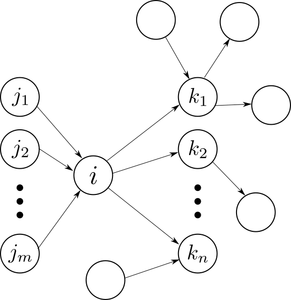
One possible way of coming up with PageRank is by modelling the surfing behavior of a user on the web graph. Imagine that at a given instant of time $latex t$ the surfer, $latex S$, is on page $latex i$. We denote this event as $latex S_t = i$. Page $latex i$ has $latex n_i$ outgoing and $latex m_i$ incoming links as depicted in the figure.

While on page $latex i$ the algorithm can do one of the following to continue navigating:

With probability $latex c$ follow randomly an outgoing link.
With probability $latex 1 - c$ select randomly an arbitrary page on the web. When this happens we say the the surfer has teleported to another page.

What happens if a page has no outgoing links? It's reasonable to assume that the user will not get stuck there forever. Instead, we will assume that it will teleport.

Now that we have a model of the user behavior let's calculate $latex P(S_t = i)$: the probability of being at page $latex i$ at time instant $latex t$. The total number of pages is $latex N$.

$latex Pleft(S_t = iright) = sum_{j=1}^N Pleft(S_{t} = i mid S_{t-1} = jright)Pleft(S_{t-1} = jright)$

Now, the probability of going from page $latex j$ to page $latex i$ is different depending on wether or not $latex j$ links to $latex i$ ($latex j rightarrow i$) or not ($latex j nrightarrow i$).

If $latex j rightarrow i$ then:

$latex Pleft(S_{t} = i mid S_{t-1} = jright) = c frac{1}{n_j} + (1 - c)frac{1}{N}$

If $latex j nrightarrow i$ but $latex n_j neq 0$ then the only possibility is that the user chooses to teleport and it lands on page $latex i$.

$latex Pleft(S_{t} = i mid S_{t-1}right) = (1 - c)frac{1}{N}$

If $latex j nrightarrow i$ and $latex n_j = 0$ then the only
possibility is that the user teleports to page $latex i$.

$latex Pleft(S_{t} = i mid S_{t-1}right) = frac{1}{N}$

We have assumed uniform probabilities in two cases: when following outgoing links all links are equally probable and also when teleporting to another page we assume all pages are equally probable. In the next section we will change this second assumption about teleporting in order to get personalized PageRank.

Putting together the above formulas we obtain after some manipulation:

$latex Pleft(S_t = iright) = c sum_{j rightarrow i} frac{P(S_{t-1} = j)}{n_j} + frac{1}{N}left(1 - csum_{n_j neq 0}P(S_{t-1} = j)right)$

Finally, for notational convenience let's call $latex pi_i^t = Pleft(S_t = iright)$:

$latex pi_i^t = c sum_{j rightarrow i} frac{pi_j^{t-1}}{n_j} + frac{1}{N}left(1 - csum_{n_j neq 0}pi_j^{t-1}right)$

PageRank is defined as the limit of the above sequence:

$latex text{PageRank}(i) = pi_i = lim_{t to infty}pi_i^t$

In practice however PageRank is computed by iterating the above formula a finite number of times, either a fixed number or until changes in the PageRank score are low enough.

If we look at the formula for $latex pi_i^t$ we see that the PageRank of a page has two parts. One part depends on how many pages are linking to the page but the other part is distributed equally to all pages. This means that all pages are going to get at least:

$latex frac{1}{N}left(1 - csum_{n_j neq 0}pi_j^{t-1}right) geq frac{1 - c}{N}$

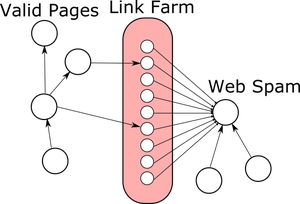
This gives an oportunity to link spammers to artificially increase the PageRank of any page they want by maintaing link farms, which are huge amounts of pages controlled by the spammer.

As PageRank will give all pages a minimum score, all of these pages will get some PageRank that can be redirected to the page the spammer wants to rise in search results.

Spammers will try to achieve a greater effect by linking from pages they don't own to either their spam page or link farm. This can be achieved since lots of pages are user-editable like blog comments, forums or wikis.

Trying to detect web spam is a never-ending war between search engines and spammers. We will now discuss Personalized PageRank as an attempt to filter out web spam. It works precisely by not giving any free score to undeserving pages.

Personalized PageRank

Personalized PageRank is obtained very similar to PageRank but instead of a uniform teleporting probability each page has its own probability $latex r_i$ of being teleported to, irrespective of the originating page:

$latex Pleft(j mathbin{text{teleports to}} i mid j: text{teleports}right) = r_i$

The update equations are therefore:
$latex pi_i^t = c sum_{j rightarrow i} frac{pi_j^{t-1}}{n_j} + r_ileft(1 - csum_{n_j neq 0}pi_j^{t-1}right)$

Of course it must be that:

$latex sum_{i=1}^N r_i = 1$

As you can see plain PageRank is just a special case where $latex r_i = 1/N$.

There are several ways the score $latex r_i$ can be calculated. For example, it could be computed using some text classification algorithm on the page content. Alternatively, it could be set to 1 for some set of seeds pages and 0 for the rest of pages, in which case we get TrustRank.

Of course, there are ways to defeat this algorithm:

Good pages can link to spam pages.
Spam pages could manage to get good scores, for example, adding certain keywords to its content (content spamming).
Link farms can be improved, for example by duplicating good pages but altering their links. Think for example mirrors of Wikipedia which add links to spam pages.

HITS

HITS (hyperlink-induced topic search) is another link analysis algorithm that assigns two scores: hub score and authority score. A page’s hub score is influenced by the authority scores of the pages linking to it, and vice versa. Twitter makes use of HITS to suggest users to follow.

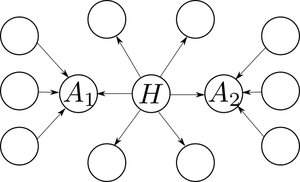
The idea is to compute for each page a pair of numbers called the hub and authority scores. Intuitively we say a page is a hub when it points to lot of pages with high authority, and we say that a page has high authority if it is pointed by many hubs.

The following graph shows one several pages with one clear hub $latex H$ and two clear authorities $latex A_1$ and $latex A_2$.

Mathematically this is expressed as:

$latex h_i = sum_{j: i to j} a_j$
$latex a_i = sum_{j: j to i} h_j$

Where $latex h_i$ represents the hub score of page $latex i$ and $latex a_i$ represents its authority score.

As with PageRank these equations are solved iteratively until they converge to the required precision. HITS was conceived as a ranking algorithm for user queries where the set of pages that were not relevant to the query were filtered out before computing HITS scores. For the purposes of our crawler we make a compromise: authority scores are modulated with the topic specific score $latex r_i$ to give the following modified equations:

$latex h_i = sum_{j: i to j} r_j a_j$
$latex a_i = sum_{j: j to i} h_j$

As we can see totally irrelevant pages ($latex r_j = 0$) don't contribute back authority.

HITS is slightly more expensive to run than PageRank because it has to maintains two sets of scores and also propagates scores twice. However it is a very interesting algorithm for crawling because by propagating scores back to the parent pages it allows to make better predictions of how good a link is likely to be and right now it's the algorithm that seems to work better, although that might be application specific.

Graph databases

The web is very much a graph, so it's natural to consider storing all of the information in a graph database. As a bonus most graph databases come with tested implementations of PageRank and in some cases HITS. Not wanting to reinvent the wheel we decided to go with GraphX as it's open source and works with HDFS. However, we decided to run the provided PageRank application on the LiveJournal dataseed, and the results were rather poor. We cancelled the job around one and a half hours in as it was already consuming 10GB of RAM.

It was surprising reading in the paper GraphChi: Large-Scale Graph Computation on Just a PC that 50 Spark nodes took half the time to compute PageRank on a graph with 40MM nodes and 1.5B edges than GraphChi on a single computer, so perhaps it didn't make sense to distribute the work. Here are some of the non-distributed libraries we tested and their timings for the LiveJournal data:

FlashGraph: 12 seconds
X-Stream: 20 seconds
SNAP: 6 minutes

Please take these timings with a grain of salt. We didn't spend any more than half an hour testing each library nor was there any fine tuning. The important thing here is the order of magnitude.

We were actually concerned we were doing something wrong while benchmarking the algorithms because the non-distributed results far exceeded the results of the distributed algorithms that it was hard to believe. However, we came across these two great blog posts that confirmed what we had found: Scalability! But at what COST? and Bigger data; same laptop. The second one is particularly interesting as it computes PageRank on a 128 billion edge graph on a single computer!

With all of this in mind we ended up implementing the database on top of a regular key/value store: LMDB. When the PageRank/HITS scores need to be recomputed, the vertex data is stored as a flat array in-memory and the links between them are streamed from the database.

We chose LMDB for the following reasons:

It's easy to deploy with just 3 source files in C, and it had a nice license.
It's fast, although for our workload other options would be faster.
Several processes can access the database simultaneously, which greatly simplifies tooling as we can access the database while the crawl is running.

Overall using LMDB and implementing the PageRank and HITS algorithms in C has been worth the effort. Even a 128 billion edge graph fits inside a 1TB disk, and the vertex data only requires around 16GB of memory. It's true that we don't have the same generality of full-blown databases or distributed computing frameworks, but for crawling the web it has been much more simple to develop and manage a non-distributed system.

Using Aduana

First install Aduana by cloning the repository and following the installation steps:

 mkdir release && cd release
 cmake .. -DCMAKE_BUILD_TYPE=Release
 make && sudo make install
 cd ../python
 python setup.py install

There's a ready to use example in Aduana's repository which you can find here.

The example implements a very simple content scorer which just counts the number of keywords in the page text without making any tokenization at all.

You can select any of the above algorithms changing the settings inside example/frontera/settings.py:

 SCORER = 'HitsScorer'
 USE_SCORES = True

Possible values for SCORER are None, PageRankScorer and HitsScorer. If any of the two latest are selected then you can decide setting USE_SCORES to True or False depending on whether you want the topic-focused or plain algorithms.

When you are satisfied with the settings and any modification you are interested in, like for example actually saving items, just run the crawler:

scrapy crawl example

You can export the crawled graph to a CSV file (actually the separator is space) even while the crawl is running:

page_db_dump info test_crawl

The fields are, in order:

URL hash
Index
URL
Time in seconds of first time the page was crawled (origin when crawl started)
Time in seconds of last crawl
Number of times the page has changed
Number of times the page has been crawled
Page content score

To get the links between pages:

page_db_dump links test_crawl

This will output a list of edges where the first element is the index of the originating page and the second element the destination page.

With the exported files you can perform whatever analysis you want with your favorite graph library, however, for convenience there are some additional tools provided.

page_db_find will output URLs and their hashes which match a given regex.

page_db_find test_crawl &lt;regex&gt;

This will output all the URLs, and their hashes, that match the given extended regex.

Finally, you can get the links, both forward and backwards of a given page with:

page_db_links test_crawl &lt;url hash&gt;

Implementing this in your own project is just a matter of including the Frontera middleware in your settings and configuring it to use the PageDB backend provided by Aduana.

You can find the relevant Frontera settings for the example in example/frontera/settings.py.

If you aren't sure how to enable Frontera in your project, here are the settings from the example:

#--------------------------------------------------------------------------
 # Frontier Settings
 #--------------------------------------------------------------------------
 SPIDER_MIDDLEWARES.update(
 {'frontera.contrib.scrapy.middlewares.schedulers.SchedulerSpiderMiddleware': 999},
 )
 DOWNLOADER_MIDDLEWARES.update(
 {'frontera.contrib.scrapy.middlewares.schedulers.SchedulerDownloaderMiddleware': 999}
 )
 SCHEDULER = 'frontera.contrib.scrapy.schedulers.frontier.FronteraScheduler'
 FRONTERA_SETTINGS = 'example.frontera.settings'

#--------------------------------------------------------------------------
# Seed loaders
#--------------------------------------------------------------------------
SPIDER_MIDDLEWARES.update({
'frontera.contrib.scrapy.middlewares.seeds.file.FileSeedLoader': 1,
})
SEEDS_SOURCE = 'seeds.txt'

The FRONTERA_SETTINGS setting refers to the settings.py file where we store the Frontera specific settings. The seeds.txt file contains a list of URLs to begin crawling with.

For more information about using Frontera, see our previous post, Frontera: The Brain Behind the Crawls.